When studying quantum systems, we naturally seek the connection between classical systems. A natural discourse is to seek the link between classical bits and qubits. In particular, we seek the answers for two questions. First, is it possible to transfer a classical bit using a quantum channel? Second, is it possible to copy an arbitrary quantum state of a quantum channel to another quantum channel? The answer two these two questions are superdense coding and quantum teleportation.

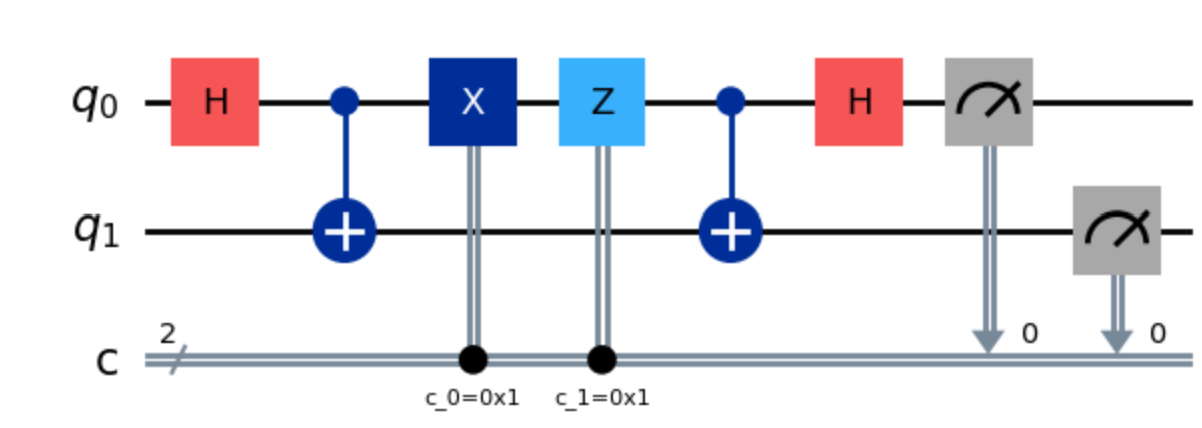
Fig 1, circuit diagram of Superdense Coding
The goal of superdense coding is to transfer two classical bits using two quantum channels. The two gates are first prepared in a bell state\[ |\beta_{00}\rangle\frac 1 {\sqrt{2}} |{00}\rangle + \frac 1 {\sqrt{2}} |{11}\rangle \]
Afterwards, an X gate and a Z gate is applied, each of which are controlled by a classical bit. Finally, the system is measured in the bell basis. The classical bit is received by the subscript of the bell basis. We list out the other three bell states.
\[ |\beta_{01}\rangle\frac 1 {\sqrt{2}} |{01}\rangle + \frac 1 {\sqrt{2}} |{10}\rangle \]
\[ |\beta_{10}\rangle\frac 1 {\sqrt{2}} |{00}\rangle – \frac 1 {\sqrt{2}} |{11}\rangle \]
\[ |\beta_{11}\rangle\frac 1 {\sqrt{2}} |{01}\rangle – \frac 1 {\sqrt{2}} |{10}\rangle \]
The first index indicates the sign change between the two states and the second index the parity.
The validation of this algorithm can be done by a brute force computation of the gate operator. Four possible inputs are possible, and upon computing the matrix representation corresponding to each input, the algorithm is verified.

Fig 2, circuit diagram of Quantum Teleportation
The quantum teleportation scheme can be considered as the reverse of superdense coding. In this process, two classical bits are transferred from the messenger to the receiver. The transferred information is further used to copy the exact quantum state of one repository to another repository.
The crux of verifying Quantum Teleportation is to express the combined state of the system after preparation and before the bell-measurement. It is straightforward to verify the following.
\[ |\psi\rangle|\beta_{00}\rangle \ = \ \frac 1 2 \left( |\beta_{00}|\rangle|\psi\rangle + |\beta_{10}\rangle |Z\psi\rangle + |\beta_{10}|\rangle|X\psi\rangle + |\beta_{11}\rangle |XZ\psi\rangle \right) \]
After the measurement, the state \(q_2\) is modified by \(X, Z\) rotations to appropriately recover the input state.
Using Quantum Teleportation, one can build a fault-tolerant controlled-X gate. In reality, \(cX\) gates are hard to implement and incurs a risk of corrupting the entire circuit. However, by teleporting the two qubits into an isolated channel, one can focus the uncertainty of the channel solely to a prepared state. The post-processing is conducted by classical logic. For more details, refer to Kaye p83.
Leave a Reply