Niobium Nitrite(NbN) is a superconducting crystal that has applications to modern quantum technology. Over the summer, I have been working on simulations of the crystal structure of this material using Density Functional Theory. The structure of an NbN crystal is a rocksalt structure, i.e. all atoms lie on the cartesian lattice of \(\mathbb R^3\). Another way to view this crystal is in the direction of the main diagonal, or in crystallographic terms, in the (111) direction. The following diagram nicely summarizes this result.
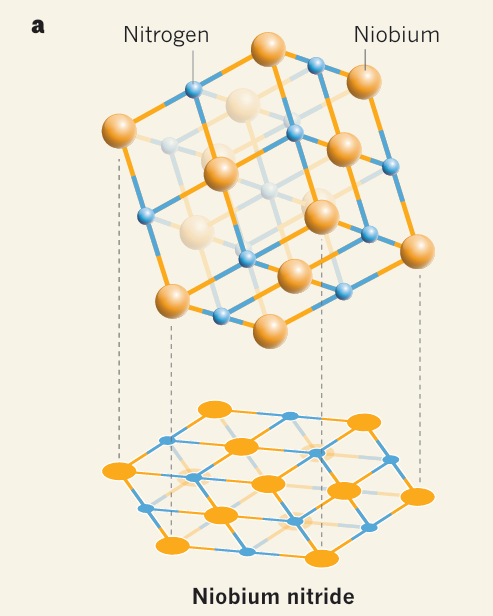
Source: Transistors driven by superconductors
The rocksalt structure viewed in the cubic conventional lattice, follows a face-centric-cubic structure with two atoms in the base. Last week, I proved mathematically, that the NbN structure can be represented as a hexagonal crystal with a 6 point base.
The next discourse was to consider the relaxation of the crystal. Given an approximate lattice parameter predicted by the crystal, it is possible to obtain a theoretical value of the exact lattice parameter using QuantumEspresso. QuantumEspresso runs simulation based on Density Functional Theory. It solves the Kohn-Sham equation, which is a simplification of the many-body Schrodinger equation, using self-consistent field approximations. To relax the crystal means to find the parameters that minimize the total energy of the crystal.
If the hexagonal representation of the crystal is valid, the crystal must retain the same structure after relaxation.
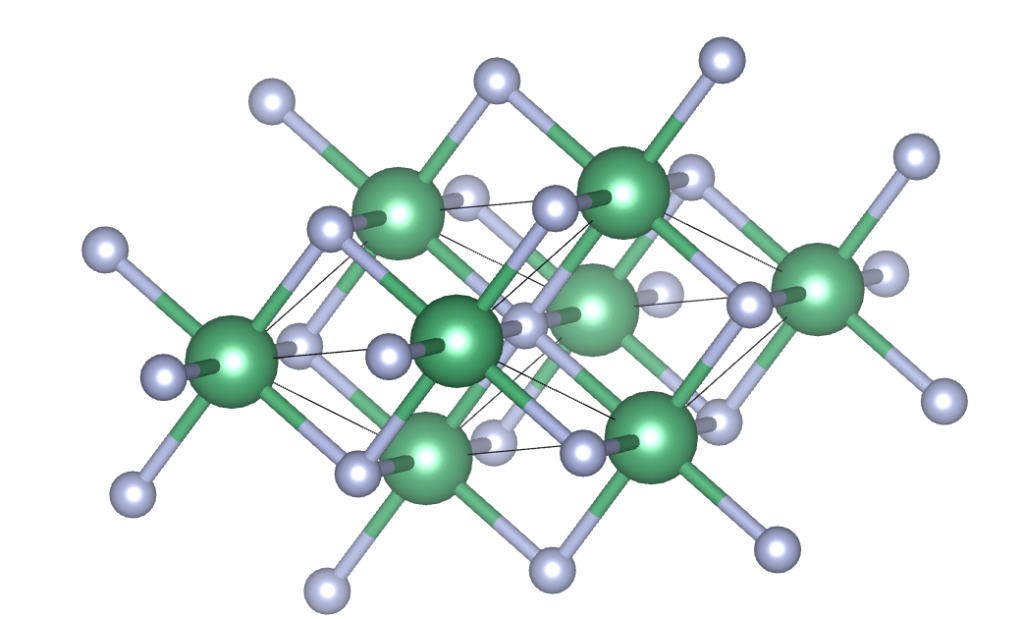
Figure: VESTA snapshot of the FCC lattice after relaxation
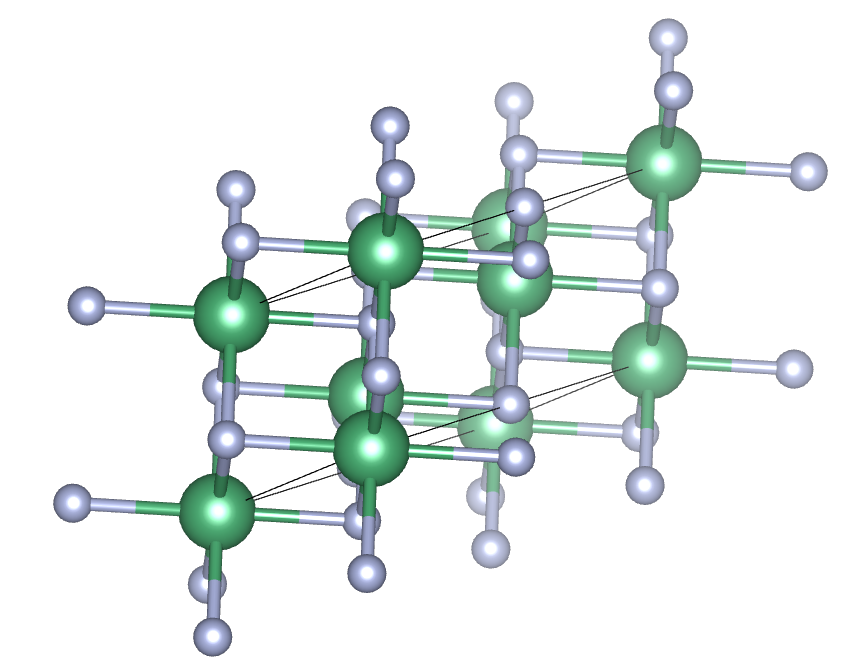
Figure: VESTA snapshot of the hexagonal lattice after relaxation
We visually verify that both the hexagonal and FCC lattice retains the rocksalt structure after relaxation. We also present the numerical results of the lattice parameters. Denoting \( a_c\) as the the lattice parameter of the fcc, i.e. the side length of one conventional unit cell, all primitive vectors of the fcc have length \(a_c/\sqrt{2}\). By simple geometry, the length and height \( a, c\) of the hexagonal lattice is respectively \( a_c / \sqrt{2}, \sqrt{3} a_c\). Using this formula along with the relaxed lattice parameters of the fcc crystal, we predict the lattice parameters of the relaxed hexagonal crystal and compare the values. Here is the result.
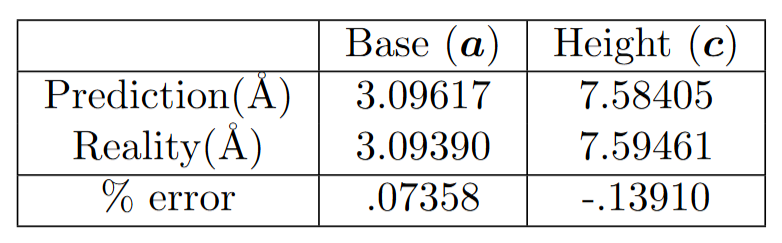
Table. Compared values of the predicted and computed lattice parameters.
This result supports the evidence that the hexagonal representation of rocksalt is valid.
Leave a Reply