Category: Uncategorized
-
On Orthogonal Matrices
Orthogonal Matrices can be considered as basis transformations in . Therefore, considering the matrix as a conglomeration of unit orthogonal column vectors, we obtain for some orthogonal matrix Q, The final equation implies a nifty equation, The following equation has interesting consequences. Suppose does not…
-
Baire Category Theorem and Applications
This post was inspired by a talk given by Professor David Damanik from Rice University. In this post, we will prove the Baire Category theorem for complete metric spaces and briefly talk about applications. Notation. Let be a metric space and . Then, denotes the open ball centered at with radius . Definition. A space…
-
A physicist approach to the delta function
The goal of this post is to convince (not prove) that the delta function can be written as an integral of a complex exponential and it satisfies the sifting property. For a formal proof, please refer to a math textbook. The main claim is that defines a delta function, and that the sifting…
-
Introduction to Semiconductor Physics Pt I. Band Plots and Effective Mass
A solid is characterized by a periodic arrangement of atoms. This periodic arrangement allows us to characterize a solid as arrangement of atoms along repeated instances of a unit cell. A single atom in a unit cell is repeatedly arranged over entire space, and this arrangement is called a lattice. To understand optical properties of…
-
Introduction to Semiconductor Physics Pt II. Law of Mass Action and Doped Semiconductors
Recall the concept of density of states from Statistical Mechanics. By filling up the reciprocal space sphere of radius and the dispersion relation , we can derive This quadratic dependence of for simple solids can be used to deduce the density of states of a semiconductor. Let denote the VBM, CBM of a…
-
Probabilistic Alterations
Probabilistic methods are extremely useful in combinatorial problems to prove an existence of certain configurations. The general approach is to take a finite probability space of configurations then to apply linearity of expectations to find the expected value of some random variable. This likely non-integral expected value is used to come up with configurations with…
-
Cutting Edges
A cutting edge refers to an edge of a graph that uniquely connects two components of a graph \(G\). More precisely, a cutting edge \(e \in G\) must satisfy \(C(G) < C(G-e)\) where the function \(C(G)\) denotes the number of components of \(G\). Proposition. An edge is a cutting edge if and only if it…
-
Why the Hamiltonian?
When I took a course in classical mechanics, I was confronted with the two mystery equations of Hamiltonian Formalism. In this post, I want to derive the two equations abiding by the subtle dependencies between quantities and the partial derivative relations. Denote the coordinates as \(q_i\) and momentum as \(p_i\). Occasionally, we will drop the…
-
Grover’s Algorithm Pt 1
We have investigated methods to learn about a given mystery quantum oracle. The Deutsch-Jozsa algorithm determines whether or not the function \(f:\{0, 1\}^n \rightarrow \{0, 1\}\) is well balanced and the Bernstein-Vazirani algorithm yields the unique string that satisfies \(f(x) = 1\). The oracle presented in the Bernstein-Vazirani algorithm provides ample information about the function…
-
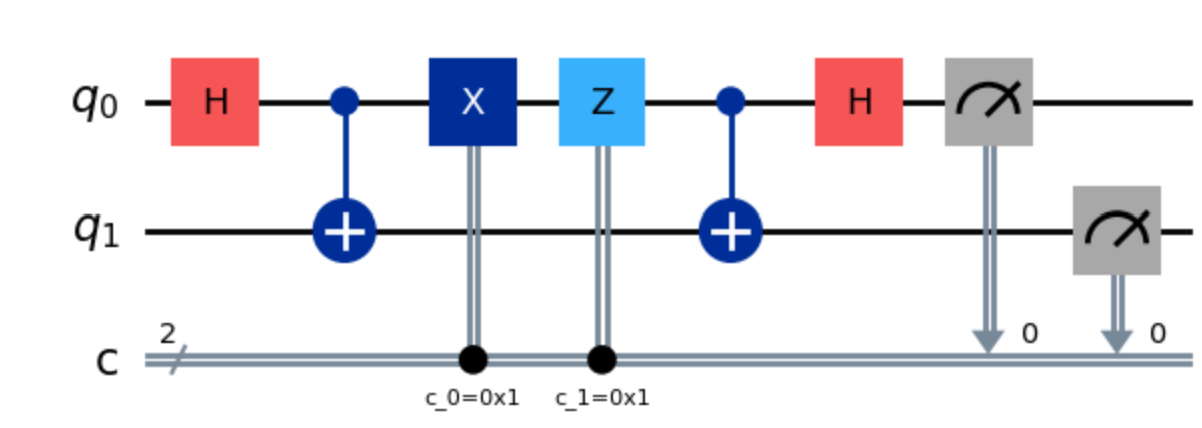
Superdense Coding and Quantum Teleportation
When studying quantum systems, we naturally seek the connection between classical systems. A natural discourse is to seek the link between classical bits and qubits. In particular, we seek the answers for two questions. First, is it possible to transfer a classical bit using a quantum channel? Second, is it possible to copy an arbitrary…