A physicist approach to the delta function

The goal of this post is to convince (not prove) that the delta function can be written as an integral of a complex exponential and it satisfies the sifting property. For a formal proof, please refer to a math textbook.

The main claim is that

$\delta(x - x') \ = \ \frac 1 {2\pi }\int_{-\infty}^\infty e^{ik(x - x')} dk$

defines a delta function, and that the sifting property works for this definition, i.e.

$\int_{-\infty}^\infty f(x)\delta(x - x') dx \ = \ f(x').$

Our approach is to define an auxillary integral

$\delta_{\alpha}(x) \ = \ \frac 1 {2\pi }\int_{-\infty}^\infty e^{-\alpha^2 + ik(x - x')} dk$

and send $\alpha \rightarrow 0$ for positive values of $\alpha$ . Completing the squares on the exponent and applying u-subsitution, the limiting integral can be expressed as a Gamma function.

$\delta_{\alpha}(x) \ = \ \frac 1 {2 \pi} \frac {e^{-(x - x')^2/(4\alpha^2)}} { \alpha} } \int _0^\infty u^{-1/2} e^{-u} du \ = \ \frac 1 {2 \pi} \frac {e^{-(x - x')^2/(4\alpha^2)}} { \alpha} } \Gamma(1/2)$

Thus,

$\delta_{\alpha}(x - x')\ = \ \frac 1 {2 \sqrt{\pi}} \frac {e^{-(x - x')^2/(4\alpha^2)}} { \alpha} }$

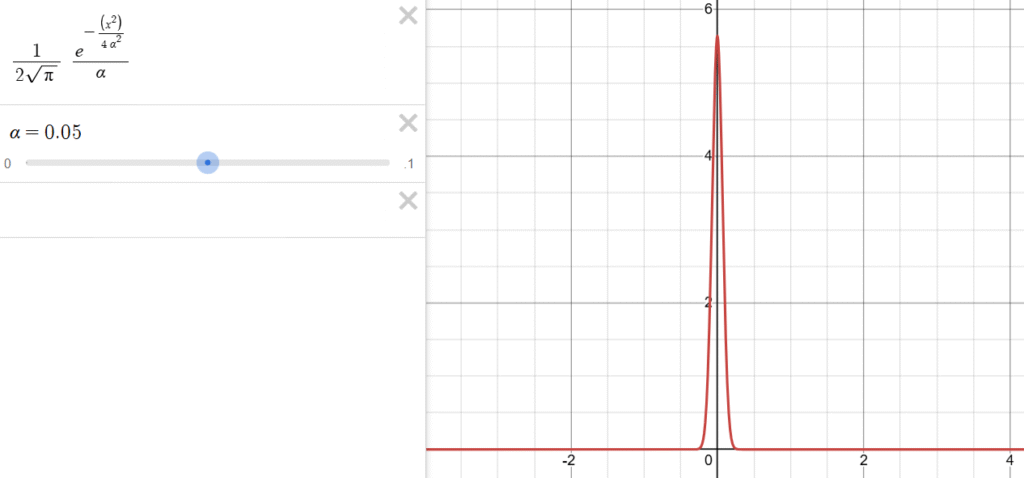
Figure: Desmos plot of a candidate limit $\delta_\alpha(x)$ at $\alpha = .05$ .

Move on to prove the sifting property. For convenience, choose $x' = 0$ and that the candidate function $f(x)$ is continuous. Outside $x = 0$ , the function $\delta_\alpha(x)$ converges uniformly to zero. Therefore,

$\int_{-\infty}^\infty f(x) \delta_\alpha (x) dx \ \rightarrow \ \int_{-\epsilon}^{\epsilon} f(x) \delta_\alpha(x) dx$

as $\alpha$ goes to $0$ , where $\epsilon > 0$ is a fixed constant. Rewrite the second integral as

$\int_{-\infty}^\infty f(x) \mathbb I _{(-\epsilon, \epsilon)} \delta_\alpha(x) dx$

and invoke Holder’s inequality for $p = 1, q = \infty$ . Each $\delta_\alpha(x)$ is normalized and integrates exactly to 1 over the real line.

(1) $\begin{align*} \int_{-\infty}^\infty (f(x) \mathbb I_{(-\epsilon, \epsilon)}(x)) \delta_\alpha(x) dx \ \leq \ \|f\cdot \mathbb I_{(-\epsilon, \epsilon)}\|_\infty \|\delta_\alpha\|_1 \ = \ f(0) \end{align*}$

On the last step, the product of the indicator and $f(x)$ was approximated to $f(0)$ assuming continuity. To show equality, prove the inequality in the other direction. Underestimate $\delta_\alpha(x)$ by a picewise linear function that is supported in the region where $\delta_\alpha(x)$ reaches a value greater than $1/e$ of its maximum height.

Since $\delta_\alpha(x)$ is concave, $u_\alpha(x) \leq \delta(x)$ by construction. We notice

$\int_{-\infty}^\infty f(x) u_\alpha(x) dx \ = \ \frac 1 {\sqrt \pi} \frac{1 + e} e f(0) \ \approx \ f(0).$

It is convincing that a better choice of a test function $u_\alpha(x)$ will give the lower bound $\int_{-\infty}^\infty f(x) \delta_\alpha (x) dx \ \geq \ f(0)$ . Combining the results, we claim

$f(0) \ = \ \int_{-\infty}^\infty f(x) \delta_\alpha (x) dx.$

Comments

Leave a Reply Cancel reply