All quantum gates correspond to a unitary operator. In fact, this implies that all the eigenvalues of a quantum gate can be described in a form of a complex exponential of the form \[\lambda \ = \ e^{i\omega}. \]
Here is a proof. Let \(U\) be the unitary operator for some quantum gate and consider the following.
\[\langle \psi | U^\dagger U |\psi\rangle \ = \ \lambda \langle \psi | U^\dagger |\psi\rangle \ = \ \lambda \lambda^* \langle \psi | |\psi\rangle \ = \ \langle \psi | I |\psi\rangle = 1\]
Necessarily, \(\|\lambda\|^2 = 1\) and hence the eigenvalue must be expressed as a complex exponential with modulus 1.
Problem. Given an arbitrary gate \(U\) along with some eigenstate \(|\psi\rangle\), retrieve the phase value \(\omega \in [0, 2\pi)\).
In fact, we know a solution to a seemingly complicated problem. The phase estimation problem can retrieve the phase factor \(\omega\) from the \(n\)-qubit state
\[|\phi_\omega\rangle \ = \ \sum_{y = 0}^{2^n – 1}\exp(2\pi i \frac {\omega y}{2^n})|y\rangle \ = \ \prod_{k = 0}^{\otimes \ n – 1} \left(\frac{|0\rangle}{\sqrt 2} + \exp(2\pi i \omega 2^k ) \frac{|1\rangle}{\sqrt 2}\right)\]
by inverse QFT.
By the idea of phase kickback, we can reenact individual terms within the tensor product by applying controlled \(U\) gates multiple times.
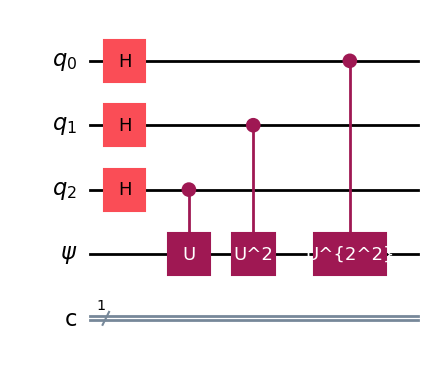
Figure. Phase encoding for \(n = 3\).
The \(U^{*}\) gate accepts \(|0\rightarrow^{\otimes 3}\) in the control registers \(q_0, q_1, q_3\) and an eigenstate of the \(U\) gate. The eigenvalues incur a phase kickback to the control registers, resulting in the state \(|\phi\rangle_\omega\otimes |\phi \rangle\). The \(c-U\) gates have encoded the eigenvalue parameter \(\omega\) as a phase factor in the control space. For simplicity, call the collection of controlled \(U\) gates without the Hadamard gate as \(U^*\).
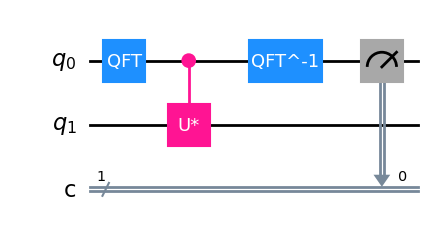
Figure. A solution for the Eigenvalue Estimation algorithm. The registers \(q_0, q_1\) are not necessarily 1-qubit channels.
We present a solution for eigenvalue estimation. Passing an input of \(|0\rangle^{\otimes n}\) to \(q_0\) and eigenstate \(|\phi\rangle\) to \(q_1\) yields a good approximation for \(\omega\) by a probability of \(8/\pi^2\) up to an uncertainty \(1/2^n\).
The collection of Hadamard gates used in the phase encoding phase is replaced to a QFT, and indeed the image of \(|0\rangle^{\otimes n}\) under the combined Hadamard gates are equal to the image of the same state under \(QFT_{2^n}\). Finally, apply the inverse QFT to the phase encoded state, successfully retrieving the phase factor \(\omega\).
Leave a Reply